Deci, aveți 9 bile și o balanță. Sau cântar. Sau balanță de greutate. Sau cum vreți să îi spuneți.
În esență, asta:
Desenul meu minunat al unei balanțe de greutate și a 9 bile
Pentru că desenez ca un copil de 2 ani, câteva clarificări cu privire la ceea ce vedeți mai sus. O balanță reală (sau cântar) arată puțin ca aparatul pe care l-am desenat mai sus. Puteți pune lucruri în micile „găleți”, iar cântarul se va înclina spre partea mai grea.
Da, probabil că nici nu ar fi trebuit să mă deranjez cu desenul. În orice caz, să trecem la ghicitoare.
1) Aveți 9 bile (așa cum se vede).
2) 8 dintre ele au exact aceeași greutate. Bila rămasă este ușor mai grea decât celelalte. Nu știți care este care.
3) Ai voie să folosești/reglezi cântarul de DOUĂ ori în total. Cu alte cuvinte, aveți ocazia să faceți aici 2 măsurători (sau „comparații”).
4) Fiecare „găleată” are suficient spațiu pentru mai multe bile. Atâta timp cât aveți același număr de bile în fiecare parte, bila grea are suficientă greutate pentru a înclina cântarul într-o parte.
Cum găsiți bila grea?
(derulați încet în jos pentru sfaturi și pentru a afla eventual răspunsul!)
.
.
.
.
Indicație #1: Nu veți pune toate bilele pentru prima măsurătoare (asta nu ar funcționa pentru că avem un număr impar!). Veți lăsa cel puțin una deoparte.
.
.
.
.
Indicație #2: În mod clar, trebuie să puneți un număr par de bile în fiecare parte pentru prima măsurătoare. Deci, fie 1+1, 2+2, 3+3 sau 4+4. Nu uitați, toate bilele au aceeași greutate, cu excepția uneia mai grele. Acesta este un amănunt important.
.
.
.
.
Indicație #3: Câte grupuri de bile puteți compara simultan? Dacă ați spus 2, mai gândiți-vă!
.
.
.
.
Indicație #4 (unul mare, și o parte din răspuns): Imaginați-vă că aveți doar 3 bile, dar nu puteți folosi cântarul decât o singură dată. Ați putea să vă dați seama care dintre cele 3 era cea mai grea? (răspunsul este da). Cum?
.
.
.
.
Indicație #5: mai jos sunt câteva culori pentru a vă ajuta….
.
.
.
.
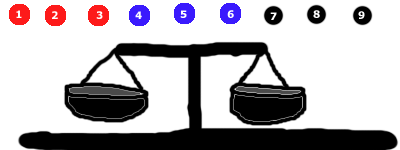
Am separat bilele în 3 grupuri. Dacă te-ai blocat, imaginea te-ar putea ajuta cu prima măsurătoare.
.
.
.
.
Indicație #6: Următoarea imagine (soluția la prima măsurătoare) este mai jos:
.
.
.
.
Începeți prin a pune 3 bile în fiecare parte. În acest caz, le lăsăm pe cele negre afară.
Se va întâmpla unul din 3 lucruri:
- The roșu partea poate coborî (caz în care știm că grupul roșu conține cea mai grea bilă), sau
- The latura albastră poate coborî (caz în care știm că grupul albastru conține cea mai grea bilă), sau
- Laturile se vor echilibra (caz în care știm că grupul negru trebuie să conțină bila cea mai grea)
În orice caz, am redus numărul de posibilități de la 9 la 3 la prima noastră măsurătoare.
Să continuăm.
.
.
.
.
De dragul argumentului, să pretindem că a fost albastru bilele care o aveau pe cea grea în măsurarea de mai sus. Să luăm 2-a și finala noastră măsurătoare.
Similar cu prima dată, le împărțim în mod egal în 3 grupuri (3 grupuri de UNA de data aceasta).
Unul dintre cele trei lucruri se va întâmpla din nou:
- Dacă #4 cade, știm că este cel greu
- Dacă #5 scade, știm că acesta este cel mai greu
- Dacă cântarul se echilibrează, știm că #6 trebuie să fie cel greu!
Gândire suplimentară (dacă a fost prea ușor pentru voi!):
Pentru a găsi bila cea mai grea am avut nevoie de 2 măsurători. De câte măsurători am avea nevoie dacă am avea 27 de bile (26 având aceeași greutate și 1 fiind mai grea)?
Dar dacă am avea 81 de bile (80 având aceeași greutate și 1 fiind mai grea)?
–
Ei bine, acesta este primul puzzle pe care îl pun din 2006 (7 ani… vai!). Sper că v-a plăcut!


Scoateți o bilă și puneți patru și patru de fiecare parte. Dacă acestea sunt echilibrate, cea pe care ați îndepărtat-o este cea mai grea.
Dacă nu sunt echilibrate, selectați cele patru din partea cea mai grea. Scoateți una și izolați.
Înlocuiți-o cu cea pe care ați eliminat-o inițial, deoarece a fost exclusă. Faceți a doua măsurătoare cu doi și doi. Dacă sunt echilibrate, cel pe care l-ați izolat este cel mai greu.
Dacă sunt dezechilibrate, pe partea unde ați înlocuit bila cunoscută. Puteți identifica cea mai grea.
Dacă sunt dezechilibrate pe cele 2 necunoscute veți avea o șansă de 50/50 de a alege corect. Această soluție oferă 3 modalități prin care ați putea fi absolut sigur.
Având în vedere: Setul A = (1, 2, 3, 4) și Setul B = (5, 6, 7, 8), iar Setul C = (9)
La măsurarea nr. 1, constatăm că setul A este mai greu decât setul B
Conform soluției dumneavoastră, eliminăm seturile B și C și împărțim setul A izolând 1 dintre bile - deci acum: Setul A=(1, 2), Setul B=(3), iar Setul C=(4).
Deoarece nu se poate compara un set de 2 bile cu un set de 1 bilă... nu ne rămâne decât să comparăm B și C în Măsura nr. 2. Dacă oricare dintre ele este mai grea, grozav...problema este rezolvată. Cu toate acestea, dacă sunt echilibrate, atunci știm că bila cea mai grea se află în setul A....și asta înseamnă să efectuăm Măsura #3.
#0 #1 #2
#3 #4 #5
#6 #7 #8
Mai întâi, comparăm greutatea monedelor din stânga (#0 #3 #6) cu cea a monedelor din dreapta (#2 #5 #8), astfel încât să știm dacă cea mai grea monedă se află în stânga, în mijloc sau în dreapta. Apoi, comparăm greutatea monedelor de sus (#0 #1 #2) cu cea a monedelor de jos (#6 #7 #8), astfel încât să știm dacă cea mai grea monedă se află în sus, în mijloc sau în jos.