Sie haben also 9 Murmeln und eine Balance. Oder eine Waage. Oder eine Waage. Oder wie auch immer Sie es nennen wollen.
Im Wesentlichen das hier:
Meine fantastische Zeichnung einer Gewichtsbalance und 9 Murmeln
Da ich wie ein 2-Jähriger zeichne, bitte ich um eine Klarstellung dessen, was Sie oben sehen. Eine reale Gewichtsbalance (oder Waage) sieht ein wenig wie der Apparat aus, den ich oben gezeichnet habe. Sie können Dinge in die kleinen „Eimer“ legen, und die Waage kippt dann auf die schwerere Seite.
Ja, ich hätte mich wahrscheinlich gar nicht erst mit dem Bild beschäftigen sollen. Wie dem auch sei, weiter zum Rätsel.
1) Sie haben 9 Murmeln (wie gesehen).
2) 8 davon haben genau das gleiche Gewicht. Die verbleibende Murmel ist etwas schwerer als die anderen. Sie wissen nicht, welche welche welche ist.
3) Sie dürfen die Waage insgesamt ZWEI Mal benutzen/einstellen. Mit anderen Worten, Sie dürfen hier 2 Messungen (oder „Vergleiche“) vornehmen.
4) Jeder „Eimer“ hat genug Platz für mehrere Murmeln. Solange Sie auf jeder Seite die gleiche Anzahl von Murmeln haben, hat die schwere Murmel gerade genug Gewicht, um die Waage auf die Seite zu kippen.
Wie finden Sie die schwere Murmel?
(scrollen Sie langsam nach unten, um Tipps und schließlich die Antwort zu erhalten!)
.
.
.
.
TIPP #1: Sie werden nicht alle Murmeln für Ihre erste Messung einsetzen (das würde nicht funktionieren, weil wir eine ungerade Zahl haben!) Sie lassen mindestens 1 Murmeln beiseite.
.
.
.
.
TIPP #2: Es ist klar, dass Sie für Ihre erste Messung eine gerade Anzahl von Murmeln in jede Seite legen müssen. Also entweder 1+1, 2+2, 3+3 oder 4+4. Vergessen Sie nicht, dass alle Murmeln das gleiche Gewicht haben, außer der 1 schwereren. Das ist ein wichtiger Leckerbissen.
.
.
.
.
TIPP #3: Wie viele Gruppen von Murmeln können Sie auf einmal vergleichen? Wenn Sie 2 gesagt haben, überlegen Sie noch einmal!
.
.
.
.
TIPP #4 (ein großer, und Teil der Antwort): Stellen Sie sich vor, Sie hätten nur 3 Murmeln, könnten aber den Maßstab nur einmal verwenden. Könnten Sie herausfinden, welche von den 3 Murmeln die schwere war? (die Antwort ist ja). Und wie?
.
.
.
.
TIPP #5: unten sind einige Farben, die Ihnen helfen sollen….
.
.
.
.
Wir haben die Murmeln in 3 Gruppen eingeteilt. Wenn Sie feststecken würden, könnte Ihnen das Bild bei Ihrer ersten Messung helfen.
.
.
.
.
Tipp #6: Das nächste Bild (Lösung zur 1. Messung) finden Sie unten:
.
.
.
.
Beginnen Sie damit, 3 Murmeln in jede Seite zu legen. In diesem Fall lassen wir die schwarzen Murmeln weg.
Eines von 3 Dingen wird passieren:
- Die rote Seite kann nach unten gehen (in diesem Fall wissen wir, dass die rote Gruppe die schwerste Murmel enthält), oder
- Die blaue Seite kann nach unten gehen (in diesem Fall wissen wir, dass die blaue Gruppe den schwersten Marmor enthält), oder
- Die Seiten werden sich ausgleichen (in diesem Fall wissen wir, dass die schwarze Gruppe die schwere Murmel enthalten muss)
So oder so haben wir es bei unserer ersten Messung von 9 Möglichkeiten auf 3 eingegrenzt.
Lassen Sie uns weitermachen.
.
.
.
.
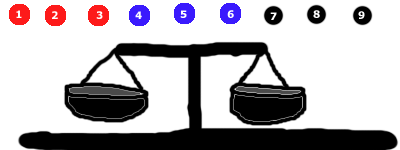
Um der Argumentation willen nehmen wir an, dass es die blauen Murmeln waren, die in der obigen Messung die schweren hatten. Nehmen wir unsere 2. und letzte Messung vor.
Ähnlich wie beim ersten Mal teilten wir diese gleichmäßig in 3 Gruppen auf (diesmal 3 Gruppen von EINER).
Eines von drei Dingen wird wieder passieren:
- Wenn #4 untergeht, wissen wir, dass es die schwere Gruppe ist.
Wenn #5 untergeht, wissen wir, dass es die Schwere ist.
Wenn die Waage das Gleichgewicht hält, wissen wir, dass #6 die schwere Waage sein muss!
Weitere Überlegungen (falls Ihnen das zu einfach war!):
Um die schwere Murmel zu finden, wurden 2 Messungen vorgenommen. Wie viele Messungen würden wir brauchen, wenn wir 27 Murmeln hätten (26 sind gleich schwer und 1 schwerer)?
Was wäre, wenn wir 81 Murmeln hätten (wobei 80 gleich schwer und 1 schwerer wäre)?
–
Nun, dies ist der erste Brain Teaser, den ich seit 2006 (7 Jahre… igitt!) aufgestellt habe. Aber es sollten bald mehr kommen. Wenn Sie diesen interessant fanden, können Sie den Abschnitt „Rätsel, Puzzles, Brain Teasers“ aufrufen, indem Sie auf die Kategorie unten klicken oder ihn im Menü oben auf der Website finden.
Entfernen Sie eine Murmel und legen Sie vier und vier eine auf jede Seite. Wenn sie ausgeglichen sind, ist diejenige, die Sie entfernt haben, die schwerste.
Wenn sie unausgeglichen sind, wählen Sie die vier von der schwereren Seite. Entfernen Sie eine und isolieren Sie sie.
Ersetzen Sie die eine durch diejenige, die Sie ursprünglich entfernt haben, weil sie ausgeschlossen wurde. Und machen Sie Ihren zweiten Takt mit zwei und zwei. Wenn sie ausgeglichen sind, ist diejenige, die Sie isoliert haben, die schwerste.
Wenn sie auf der Seite unausgeglichen sind, auf der Sie die bekannte Murmel ersetzt haben, ist die, die Sie isoliert haben, die schwerste. Sie können den schwersten identifizieren.
Wenn sie auf der 2 unbekannten Seite unausgewogen sind, haben Sie eine 50/50-Chance, richtig zu wählen. Diese Lösung bietet 3 Möglichkeiten, wie Sie absolut sicher sein können.
Gegeben: Menge A = (1, 2, 3, 4) und Menge B = (5, 6, 7, 8), und Menge C = (9)
Bei Messung Nr. 1 stellen wir fest, dass Menge A schwerer ist als Menge B
Gemäß Ihrer Lösung verwerfen wir die Mengen B und C und teilen die Menge A auf, indem wir 1 der Murmeln isolieren - also jetzt: Menge A=(1, 2), Menge B=(3), und Menge C=(4).
Da man eine Menge von 2 Murmeln nicht mit einer Menge von 1 Murmel vergleichen kann, bleibt nur der Vergleich von B & C in Messung #2. Wenn eine der beiden schwerer ist, großartig...das Problem ist gelöst. Wenn sie jedoch ausgeglichen sind, dann wissen wir, dass die schwere Murmel in Satz A.... ist und das bedeutet, dass wir Messung Nr. 3 durchführen müssen.