所以,你有9个弹珠和一个天平。或者称体重秤。或者称体重平衡。或者随便你怎么叫它。
本质上,这是:
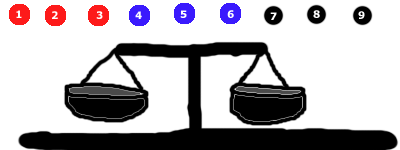
因为我画画就像两岁小孩,所以需要解释一下上面画的东西。真正的重量平衡(或称天平)看起来和我上面画的装置有点像。你可以把东西放在小”桶”里,天平就会向较重的一侧倾斜。
是的,我可能根本不应该画这幅画。无论如何,谜题来了。
1) 你有9个弹珠(如图所示)。
2) 其中8个重量完全相同。剩下的一个比其他的稍微重一些。你不知道哪个是哪个。
3) 您总共可以使用/设置天平两次。换句话说,您可以在这里进行两次测量(或”比较”)。
4) 每个”桶”都有足够的空间容纳多个大理石。只要每侧的大理石数量相同,那么重的大理石就足以使天平倾斜。
如何找到较重的大理石?
(向下慢慢滚动,查看提示,最终找到答案!)。
。
。
。
提示1:第一次测量时,您不会把所有的弹珠都放入秤盘(那样做是行不通的,因为我们的数字是奇数!)。您至少要留出1个弹珠。.
.
.
提示2:显然,第一次测量时,每侧必须放上偶数个弹珠。所以要么是1+1、2+2、3+3,要么是4+4。别忘了,除了一个较重的弹珠外,其他弹珠的重量都一样。这是一个重要的细节。.
.
.
.
提示3:你能同时比较几组弹珠?如果你说是2组,再想想!.
.
.
.
提示4(非常重要,也是答案的一部分):假设你只有3个弹珠,但只能使用一次天平。你能找出3个弹珠中哪个最重吗?(答案是肯定的)。怎么做?.
.
.
.
提示5:以下是一些颜色,可以帮助你…….
.
.
我们将弹珠分为3组。如果您遇到了困难,图片可以帮助您进行第一次测量。.
.
.
提示6:下一张图片(第一次测量的解决方案)如下:.
.
.
.
首先,在每侧放3个弹珠。在这种情况下,我们不用黑色的。
会发生以下三种情况之一:
- 红色一侧可能会下降(在这种情况下,我们知道红色组包含最重的大理石),或者
- 蓝色一侧可能会下沉(在这种情况下,我们知道蓝色组包含最重的大理石),或者
- 两边会平衡(在这种情况下,我们知道黑色组必须包含重的大理石)
无论哪种方式,我们第一次测量就将9种可能性缩小到了3种。
让我们继续。.
.
。。
为了论证起见,我们假设在上面的测量中,蓝色的大理石块比较重。让我们进行第二次也是最后一次测量。
与第一次一样,我们将它们平均分成3组(这次是3组1个)。
三种情况中的一种将再次发生:
- 如果#4掉下来,我们知道它是较重的
- 如果#5掉下来,我们知道它是较重的
- 如果天平平衡,我们知道#6一定是重的那颗!
进一步思考(如果这对您来说太简单了!):
找到最重的大理石需要测量两次。如果我们有27个大理石(26个重量相同,1个更重),我们需要测量几次?
如果我们有81个大理石(80个重量相同,1个更重),又该怎么办?
–
这是自2006年以来我提出的第一个脑筋急转弯(7年了……)。希望您喜欢!



* 我们首先将弹珠分成 3 组。我们想看看哪个组包含重弹珠。为此,请在每侧放置 3 个弹珠(左 3 个,右 3 个,未使用)
* 如果天平向一侧倾斜,我们知道 3 组有沉重的弹珠。如果它没有向一侧倾斜(如果它平衡),我们就知道“未使用”的 3 组包含沉重的弹珠。保留较重的 3 颗弹珠,丢弃其余的。
* 由于我们现在有 3 个弹珠(其中 1 个是较重的弹珠),因此每侧放置 1 个(1 个左,1 个右,1 个未使用)
* 再次设置比例。如果它向一侧倾斜,我们知道大理石很重!如果它是平衡的,我们知道“未使用”的大理石是沉重的大理石!
取出 1 颗弹珠,放入 4 颗和 4 颗,每边放一颗。如果它们是平衡的,则您删除的那个是最重的。
如果它们不平衡,请从较重的一侧中选择四个。取出一个并隔离。
将该 ID 替换为您最初删除的 URL,因为它已被排除。然后用 2 和 2 进行第二次测量。如果它们是平衡的,则您隔离的那个是最重的。
如果它们在您替换已知弹珠的一侧不平衡。您可以确定最重的。
如果他们在 2 个未知数上不平衡,您将有 50/50 的机会正确选择。该解决方案提供了 3 种您可以绝对确定的方法。
给定: 集合 A = (1, 2, 3, 4) 和集合 B = (5, 6, 7, 8),集合 C = (9)
在测量 #1 中,我们发现集合 A 比集合 B 重
根据您的解决方案,我们丢弃集合 B 和 C,并通过分离 1 个弹珠来拆分集合 A——所以现在:集合 A=(1, 2),集合 B=(3) 和集合 C=(4)。
由于您无法将一组 2 个弹珠与一组 1 个弹珠进行比较......我们只剩下在测量#2中比较B和C。 如果其中任何一个更重,那就太好了......问题解决了。 但是,如果它们是平衡的,那么我们就知道沉重的弹珠在集合 A 中......这意味着进行测量 #3。
硬币的排列方式如下:
#0 #1 #2
#3 #4 #5
#6 #7 #8
首先,我们比较左边硬币 (#0 #3 #6) 和右边硬币 (#2 #5 #8) 的重量
因此,我们知道最重的硬币是在左边、中间还是右边。
然后,我们比较顶部硬币 (#0 #1 #2) 和底部硬币 (#6 #7 #8) 的重量
所以我们知道最重的硬币是在顶部、中间还是底部。
然后我们通过坐标找到硬币。