所以,你有 9 顆彈珠和一個天平。或稱重天平。或者重量天平。或者隨便你怎麼稱呼它。
基本上就是這樣
因為我畫得像個兩歲小孩,所以要澄清一下您在上面看到的東西。真正的天平(或磅秤)看起來和我上面畫的器具有點像。您可以在小 「桶 」裡放一些東西,然後秤就會向較重的一邊傾斜。
是啊,我可能根本就不該費心畫這張圖。無論如何,開始猜謎語。
1) 您有 9 顆彈珠 (如圖)。
2) 其中 8 顆重量完全相同。剩餘的彈珠比其他的稍重。您不知道哪顆是哪顆。
3) 您總共可以使用/設定天平兩次。換句話說,您可以在這裡進行兩次測量(或「比較」)。
4) 每個「桶」都有足夠的空間放置多顆彈珠。只要兩邊的彈珠數量相同,重的彈珠就有足夠的重量讓天平傾側。
如何找到重的彈珠?
(慢慢向下捲動以獲得提示,並最終得到答案!)
.
.
.
.
提示 #1:第一次測量時,您不會把所有彈珠都放進去 (那是不行的,因為我們的數量是奇數!)。您至少要留一顆在一旁。
.
.
.
.
提示 #2:很明顯的,您必須在第一次測量時,每邊放偶數顆彈珠。所以可以是 1+1、2+2、3+3 或 4+4。別忘了,除了 1 顆較重的彈珠之外,所有彈珠的重量都是一樣的。這是一個重要的花絮.
.
.
.
.
提示 #3:您可以同時比較幾組彈珠?如果您說 2,請再想一想!
.
.
.
.
提示 #4(一個很大的提示,也是答案的一部分): 假設您只有三顆彈珠,但只能使用一次刻度。您能找出三顆彈珠中哪顆是重的嗎?(答案是肯定的)。如何計算?
.
.
.
.
提示 #5:以下是一些顏色可以幫助您….
.
.
.
.
我們將彈珠分成 3 組。如果您卡住了,這幅圖可能會幫助您完成第一次測量。
.
.
.
.
提示 #6:下一張圖片(第一次測量的解決方案)如下:
.
.
.
.
開始時,每邊放 3 顆彈珠。在這種情況下,我們不放黑色的彈珠。
有三種情況會發生
- 紅色一方可能會倒下(在這種情況下,我們知道 紅色群組包含最重的彈珠),或
- 藍色一側可能會掉落(在這種情況下,我們知道藍色組包含最重的彈珠),或者
- 兩邊會平衡(在這種情況下,我們知道黑色這組一定包含重的彈珠)
無論如何,我們已經從第一次測量的 9 種可能性縮小到 3 種。
讓我們繼續。
.
.
.
.
.
為了爭論起見,我們假設是 藍色彈珠在上述量測中較重。讓我們進行 第 2 次和 最後的量測。
和第一次類似,我們把這些平均分成 3 組(這次是 3 組 ONE)。
有三種情況之一會再次發生
- 如果 #4倒下,我們就知道它是重物
- 如果 #5 下降,我們知道它是重的那個
- 如果天秤平衡,我們知道 #6一定是重的!
進一步思考(如果這對您來說太容易了!):
找到重的彈珠需要量兩次。如果我們有 27 顆彈珠 (26 顆重量相同,1 顆較重),我們需要多少次量測?
如果我們有 81 顆彈珠(80 顆重量相同,1 顆較重)呢?
–
這是我自 2006 年(7 年了……哎呀!)以來的第一個腦筋急轉彎。希望您喜歡!
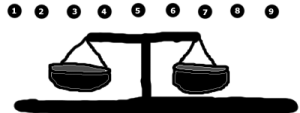
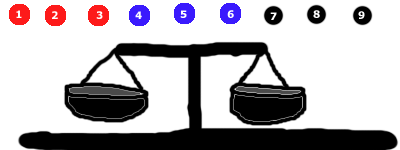


* 我們首先將彈珠分成 3 組。我們想看看哪個組包含重彈珠。為此,請在每側放置 3 個彈珠(左 3 個,右 3 個,未使用)
* 如果天平向一側傾斜,我們知道 3 組有沉重的彈珠。如果它沒有向一側傾斜(如果它平衡),我們就知道“未使用”的 3 組包含沉重的彈珠。保留較重的 3 顆彈珠,丟棄其餘的。
* 由於我們現在有 3 個彈珠(其中 1 個是較重的彈珠),因此每側放置 1 個(1 個左,1 個右,1 個未使用)
* 再次設定比例。如果它向一側傾斜,我們知道大理石很重!如果它是平衡的,我們知道「未使用」的大理石是沉重的大理石!
取出 1 顆彈珠,放入 4 顆和 4 顆,每邊放一顆。如果它們是平衡的,則您刪除的那個是最重的。
如果它們不平衡,請從較重的一側中選擇四個。取出一個並隔離。
將該 ID 替換為您最初刪除的 URL,因為它已被排除。然後用 2 和 2 進行第二次測量。如果它們是平衡的,則您隔離的那個是最重的。
如果它們在您替換已知彈珠的一側不平衡。您可以確定最重的。
如果他們在 2 個未知數上不平衡,您將有 50/50 的機會正確選擇。該解決方案提供了3種您可以絕對確定的方法。
給定: 集合 A = (1, 2, 3, 4) 和集合 B = (5, 6, 7, 8),集合 C = (9)
在測量 #1 中,我們發現集合 A 比集合 B 重
根據您的解決方案,我們丟棄集合 B 和 C,並通過分離 1 個彈珠來拆分集合 A——所以現在:集合 A=(1, 2),集合 B=(3) 和集合 C=(4)。
由於您無法將一組 2 個彈珠與一組 1 個彈珠進行比較......我們只剩下在測量#2中比較B和C。 如果其中任何一個更重,那就太好了......問題解決了。 但是,如果它們是平衡的,那麼我們就知道沉重的彈珠在集合 A 中......這意味著進行測量 #3。
硬幣的排列方式如下:
#0 #1 #2
#3 #4 #5
#6 #7 #8
首先,我們比較左邊硬幣 (#0 #3 #6) 和右邊硬幣 (#2 #5 #8) 的重量
因此,我們知道最重的硬幣是在左邊、中間還是右邊。
然後,我們比較頂部硬幣 (#0 #1 #2) 和底部硬幣 (#6 #7 #8) 的重量
所以我們知道最重的硬幣是在頂部、中間還是底部。
然後我們通過座標找到硬幣。