Отже, у вас є 9 кульок і терези. Або ваги. Або гиря. Або як завгодно називайте це.
По суті, це:
Мій дивовижний малюнок ваги і 9 кульок.
Оскільки я малюю, як 2-річна дитина, деякі пояснення щодо того, що ви бачите вище. Справжні терези (або ваги) виглядають дещо схожими на пристрій, який я намалював вище. Ви можете покласти речі в маленькі “відерця”, і шальки терезів перехиляться на більш важку сторону.
Так, напевно, не варто було навіть морочитися з малюнком. У будь-якому випадку, перейдемо до загадки.
1) У вас є 9 кульок (як ми бачимо).
2) 8 з них мають точнооднакову вагу. Останній камінчик трохи важчий за інші. Ви не знаєте, який з них важчий.
3) Всього вам дозволено використовувати/встановлювати ваги ДВІЧІ. Іншими словами, ви можете зробити 2 вимірювання (або “порівняння”).
4) У кожному “відерці” достатньо місця для кількох кульок. Якщо у вас однакова кількість камінців у кожній стороні, то важкий камінчик має достатню вагу, щоб перехилити шальки терезів на свій бік.
Питання;
Як знайти важкий камінь?
(повільно прокрутіть сторінку вниз, щоб отримати підказки і врешті-решт знайти відповідь!).
.
.
.
.
Підказка №1: Ви не будете класти всі камінці для першого вимірювання (це не спрацює, оскільки у нас непарна кількість!). Ви повинні залишити принаймні 1 камінчик в стороні.
.
.
.
.
Підказка №2: Очевидно, що для першого вимірювання вам потрібно покласти парну кількість камінців у кожну сторону. Тобто 1+1, 2+2, 3+3 або 4+4. Не забувайте, що всі камінці мають однакову вагу, окрім 1 важчого. Це дуже важлива деталь.
.
.
.
.
Підказка №3: Скільки груп кульок можна порівняти одночасно? Якщо Ви сказали 2, подумайте ще раз!
.
.
.
.
Підказка №4 (велика і є частиною відповіді): Уявіть, що у вас було лише 3 кульки, але ви могли скористатися терезами лише один раз. Чи могли б ви визначити, яка з 3 кульок була найважчою? (відповідь “так”). Як?
.
.
.
.
Підказка №5: нижче наведено кілька кольорів, які допоможуть вам….
.
.
.
.
Ми розділили кульки на 3 групи;
Ми розділили кульки на 3 групи. Якщо ви застрягли, малюнок може допомогти вам при першому вимірюванні.
.
.
.
.
Підказка №6: Наступне зображення (розв’язок для 1-го виміру) знаходиться нижче:
.
.
.
.
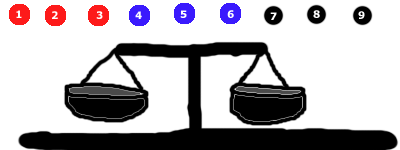
Починайте;
Почніть з того, що покладіть по 3 камінці в кожну сторону. У цьому випадку ми залишаємо чорні камінці поза увагою.
Відбудеться одна з 3 подій:
- Червона сторона червона сторона може опуститися вниз (у цьому випадку ми знаємо, що червона група містить найважчий мармур), або
- Сама синя сторона може піти вниз (у цьому випадку ми знаємо, що синя група містить найважчий мармур), або
- Сторони будуть балансувати (у цьому випадку ми знаємо, що чорна група повинна містити найважчий мармур)
У будь-якому випадку, ми звузили список з 9 варіантів до 3 під час першого вимірювання.
Давайте продовжимо.
.
.
.
.
Для прикладу, уявімо, що це були синій камінчик був найважчим у наведеному вище вимірі. Візьмемо наш 2-й і останній виміри.
Другий вимір;
Як і в перший раз, ми розділимо їх рівномірно на 3 групи (цього разу 3 групи по ОДИН).
Знову станеться одна з трьох подій:
- Якщо №4 падає, ми знаємо, що він найважчий
- Якщо №5 падає вниз, ми знаємо, що це важкий
- Якщо шальки терезів врівноважуються, ми знаємо, що №6 має бути найважчий!
Далі міркуємо (якщо це було занадто просто для вас!)::
Щоб знайти найважчий мармур, знадобилося 2 вимірювання. Скільки вимірювань нам знадобилося б, якби у нас було 27 камінчиків (26 однакової ваги і 1 важчий)?
А якщо б у нас був 81 камінчик (80 однакової ваги і 1 важчий)?
–
Що ж, це перша головоломка, яку я опублікував з 2006 року (7 років… ой!). Сподіваюсь, вам сподобалось!


Приберіть один камінчик і покладіть чотири, по чотири з кожного боку. Якщо вони врівноважені, то той, який ви вийняли, буде найважчим.
Якщо вони не збалансовані, виберіть чотири з важчої сторони. Вийміть один і ізолюйте його.
Замініть його на той, який ви спочатку прибрали, тому що він був виключений. І зробіть другий вимір з двома і двома. Якщо вони збалансовані, то той, який ви ізолювали, буде найважчим.
Якщо вони не збалансовані, то з того боку, куди ви поклали відомий мармур, - важчий. Ви можете визначити найважчий.
Якщо вони не врівноважені на 2 невідомих, у вас буде 50/50 шансів зробити правильний вибір. Це рішення пропонує 3 способи, які дають вам абсолютну впевненість.
Нехай задано Множина A = (1, 2, 3, 4), множина B = (5, 6, 7, 8) і множина C = (9)
При вимірюванні №1 ми бачимо, що множина A важча за множину B
Згідно з вашим розв'язком, ми відкидаємо множини B і C і розбиваємо множину A, ізолювавши 1 камінчик - отже, тепер: Множина A=(1, 2), множина B=(3) і множина C=(4).
Оскільки ви не можете порівняти множину з 2 камінців з множиною з 1 камінця... нам залишається лише порівняти B та C у Вимірюванні #2. Якщо один з них важчий, чудово... проблема вирішена. Однак, якщо вони врівноважені, то ми знаємо, що важчий камінчик знаходиться в наборі A...., а це означає, що потрібно зробити вимір №3.
#0 #1 #2
#3 #4 #5
#6 #7 #8
Спочатку ми порівнюємо вагу лівих монет (#0 #3 #6) і правих (#2 #5 #8), щоб дізнатися, де знаходиться найважча монета - зліва, посередині чи справа. Потім ми порівнюємо вагу верхніх монет (#0 #1 #2) і нижніх (#6 #7 #8), щоб дізнатися, де знаходиться найважча монета - зліва, посередині чи знизу. Після цього ми знайдемо цю монету за її координатою.