Итак, у вас есть 9 шариков и весы. Или весы. Или весы. Или как вы хотите это назвать.
По сути, это:
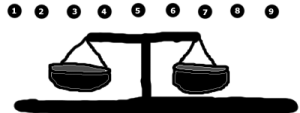
Мой потрясающий рисунок весов и 9 шариков.
Поскольку я рисую как двухлетний ребенок, немного пояснений к тому, что вы видите выше. Настоящие весы (или гири) выглядят примерно так же, как и те, что я нарисовал выше. Вы можете класть предметы в маленькие «ведерки», и весы будут склоняться в сторону большего веса.
Да, наверное, мне не стоило даже беспокоиться об этом рисунке. В любом случае, перейдем к загадке.
1) У вас есть 9 шариков (как видно).
2) 8 из них имеют одинаковый вес. Оставшийся мрамор чуть тяжелее остальных. Вы не знаете, какой из них какой.
3) Всего вам разрешено использовать/устанавливать весы ДВА раза. Другими словами, вы можете провести 2 измерения (или «сравнения»).
4) В каждом «ведерке» достаточно места для нескольких шариков. При одинаковом количестве шариков в каждой стороне, тяжелый мрамор имеет достаточный вес, чтобы опрокинуть весы на бок.
Как найти тяжелый мрамор?
(медленно прокрутите страницу вниз, чтобы получить подсказки и узнать ответ!)
.
.
.
.
Подсказка №1: Вы не будете класть все шарики для первого измерения (это не сработает, потому что у нас нечетное число!). Вы оставите хотя бы 1 в стороне.
.
.
.
.
Подсказка №2: Очевидно, что для первого измерения вам нужно положить четное количество шариков в каждую сторону. То есть либо 1+1, либо 2+2, либо 3+3, либо 4+4. Не забывайте, что все шарики имеют одинаковый вес, за исключением одного более тяжелого. Это важный момент.
.
.
.
.
Подсказка №3: Сколько групп шариков вы можете сравнить одновременно? Если вы сказали 2, подумайте еще раз!
.
.
.
.
Подсказка №4 (большая и часть ответа): Представьте, что у вас всего 3 шарика, а весы можно использовать только один раз. Сможете ли вы определить, какой из трех шариков тяжелее? (Ответ — да). Как?
.
.
.
.
Подсказка №5: ниже приведены некоторые цвета, которые помогут вам…..
.
.
.
.
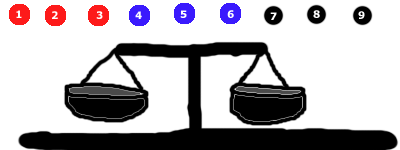
Мы разделили шарики на 3 группы. Если вы застряли, картинка может помочь вам с первым измерением.
.
.
.
.
Подсказка №6: Следующая картинка (решение 1-го измерения) находится ниже:
.
.
.
.
Начните с того, что положите по 3 шарика на каждую сторону. В данном случае мы оставим черные.
Произойдет одно из трех событий:
- Страна красная сторона может опуститься (в этом случае мы знаем, что красная группа содержит самый тяжелый мрамор), или
- Строка синяя сторона может опуститься (в этом случае мы знаем, что синяя группа содержит самый тяжелый мрамор), или
- Стороны будут балансироваться (в этом случае мы знаем, что черная группа должна содержать тяжелый мрамор)
В любом случае мы сократили число возможных вариантов с 9 до 3 при первом измерении.
Давайте продолжим.
.
.
.
.
Для примера представим, что именно синие шарики, которые были тяжелыми в измерении выше. Возьмем наши второе и окончательное измерения.
Как и в первый раз, мы разделим их поровну на 3 группы (на этот раз 3 группы по ОДНОМУ).
Снова произойдет одно из трех событий:
- Если №4 падает, мы знаем, что он тяжелый
- Если №5 опускается, мы знаем, что он самый тяжелый
- Если весы уравновешиваются, мы знаем, что №6 должен быть тяжелым!
Дальнейшее размышление (если это было слишком просто для вас!):
Чтобы найти тяжелый мрамор, потребовалось 2 измерения. Сколько измерений нам понадобится, если у нас будет 27 шариков (26 одинакового веса и один тяжелее)?
А если бы у нас был 81 шарик (80 одинаковых по весу и 1 более тяжелый)?
—
Что ж, это первая головоломка, которую я разместил с 2006 года (7 лет… ух!). Надеюсь, вам понравилось!


Уберите один мрамор и положите четыре и четыре с каждой стороны. Если они сбалансированы, тот, который вы убрали, будет самым тяжелым.
Если они не сбалансированы, выберите четыре с более тяжелой стороны. Удалите один и изолируйте его.
Замените его тем, который вы изначально удалили, потому что он был исключен. Проведите второе измерение с двумя и двумя. Если они сбалансированы, тот, кого вы выделили, будет самым тяжелым.
Если они не сбалансированы, то на той стороне, где вы заменили известный мрамор. Вы можете определить самый тяжелый.
Если они не уравновешены на 2 неизвестных, то вероятность правильного выбора будет 50/50. Это решение дает 3 способа быть абсолютно уверенным.
Дано: Набор A = (1, 2, 3, 4), Набор B = (5, 6, 7, 8) и Набор C = (9).
При измерении №1 выясняется, что набор A тяжелее набора B.
Согласно вашему решению, мы отбрасываем наборы B и C и разбиваем набор A, изолируя 1 из шариков - так что теперь: Набор A=(1, 2), Набор B=(3) и Набор C=(4).
Поскольку вы не можете сравнить набор из 2 шариков с набором из 1 шарика... нам остается только сравнить B и C в Измерении №2. Если один из них тяжелее, отлично... проблема решена. Однако если они уравновешены, то мы знаем, что тяжелый мрамор находится в наборе A...., а это означает, что нужно сделать Измерение #3.
#0 #1 #2
#3 #4 #5
#6 #7 #8
) с правыми (#2 #5 #8), чтобы знать, где находится самая тяжелая монета - слева, посередине или справа. Затем мы сравниваем вес верхних монет (#0 #1 #2) с нижними (#6 #7 #8), чтобы знать, где находится самая тяжелая монета - сверху, посередине или снизу. Затем мы находим монету по координатам.