Je hebt dus 9 knikkers en een weegschaal. Of weegschaal. Of weegschaal. Of hoe je het ook wilt noemen.
In wezen, dit:
Mijn geweldige tekening van een weegschaal en 9 knikkers.
Omdat ik teken als een 2-jarige, even wat uitleg over wat je hierboven ziet. Een echte weegschaal lijkt een beetje op het apparaat dat ik hierboven heb getekend. Je kunt dingen in de kleine “emmers” doen en de weegschaal kantelt naar de zwaardere kant.
Ja, ik had waarschijnlijk niet eens de moeite moeten nemen om een plaatje te maken. In ieder geval, over naar het raadsel.
1) Je hebt 9 knikkers (zoals gezien).
2) 8 daarvan zijn exact hetzelfde gewicht. De overgebleven knikker is lichtjes zwaarder dan de anderen. Je weet niet welke welke is.
3) Je mag de weegschaal in totaal TWEE keer gebruiken. Met andere woorden, je mag hier 2 metingen (of “vergelijkingen”) doen.
4) Elke “emmer” heeft genoeg ruimte voor meerdere knikkers. Zolang je hetzelfde aantal knikkers in elke kant hebt, heeft de zware knikker net genoeg gewicht om de weegschaal op zijn kant te doen kantelen.
Hoe vind je de zware knikker?
(scroll langzaam naar beneden voor tips en eventueel het antwoord!).
.
.
.
.
Hint #1: Je doet niet alle knikkers in je eerste meting (dat zou niet werken omdat we een oneven aantal hebben!). Je laat er minstens 1 opzij.
.
.
.
.
Hint #2: Het is duidelijk dat je een even aantal knikkers aan elke kant moet leggen voor je eerste meting. Dus ofwel 1+1, 2+2, 3+3, of 4+4. Vergeet niet dat alle knikkers hetzelfde gewicht hebben, behalve de 1 zwaardere. Dat is een belangrijk weetje.
.
.
.
.
Hint #3: Hoeveel groepen knikkers kun je tegelijk vergelijken? Als je 2 zei, denk dan nog eens na!
.
.
.
.
Hint #4 (een grote, en een deel van het antwoord): Doe alsof je maar 3 knikkers had, maar de weegschaal maar één keer kon gebruiken. Zou je kunnen achterhalen welke van de 3 de zwaarste was? (Het antwoord is ja). Hoe?
.
.
.
.
Hint #5: hieronder staan enkele kleuren om je te helpen….
.
.
.
.
We hebben de knikkers in 3 groepen verdeeld. Als je vast zat, kan de afbeelding je helpen met je eerste meting.
.
.
.
.
Hint #6: De volgende afbeelding (oplossing voor de 1e meting) staat hieronder:
.
.
.
.
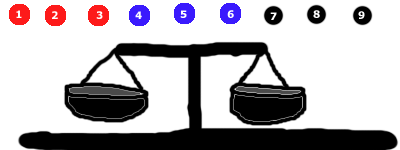
Begin met 3 knikkers aan elke kant te leggen. In dit geval laten we de zwarte knikkers weg.
Een van de 3 dingen zal gebeuren:
- De rode kant kan naar beneden gaan (in dat geval weten we dat de rode groep de zwaarste knikker bevat), of
- De blauwe kant kan naar beneden gaan (in dat geval weten we dat de blauwe groep de zwaarste knikker bevat), of
- De zijden zullen in evenwicht (in dat geval weten we dat de zwarte groep het zware marmer moet bevatten)
Hoe dan ook, we hebben het aantal mogelijkheden teruggebracht van 9 naar 3 bij onze eerste meting.
Laten we doorgaan.
.
.
.
.
Laten we omwille van het argument doen alsof de blauwe knikkers de zwaarste waren in de meting hierboven. Laten we onze 2nd en final meting nemen.
Net als de eerste keer verdelen we deze gelijkmatig in 3 groepen (3 groepen van EEN deze keer).
Een van de drie dingen zal weer gebeuren:
- Als #4 gaat neer, dan weten we dat het de zware is
- Als #5 naar beneden gaat, weten we dat dit de zware is
- Als de weegschaal in evenwicht is, weten we dat #6 de zwaarste moet zijn!
Verder nadenken (als dat te makkelijk voor je was!):
Om de zware knikker te vinden waren 2 metingen nodig. Hoeveel metingen zouden we nodig hebben als we 27 knikkers hadden (26 van hetzelfde gewicht en 1 zwaarder)?
Wat als we 81 knikkers hadden (80 even zwaar en 1 zwaarder)?
–
Dit is de eerste breinbreker sinds 2006 (7 jaar… jakkes!). Hopelijk vond je het leuk!


Verwijder een knikker en leg er vier en vier aan elke kant. Als ze in evenwicht zijn, is degene die je hebt verwijderd de zwaarste.
Als ze niet in evenwicht zijn, kies dan de vier van de zwaarste kant. Verwijder er één en isoleer.
Vervang die door degene die je oorspronkelijk hebt verwijderd omdat die is uitgesloten. En doe je tweede meting met twee en twee. Als ze in balans zijn, is degene die je hebt geïsoleerd de zwaarste.
Als ze niet in evenwicht zijn aan de kant waar je de bekende knikker hebt vervangen. Je kunt de zwaarste identificeren.
Als de 2 onbekende knikkers niet in evenwicht zijn, heb je 50/50 kans om de juiste keuze te maken. Deze oplossing biedt 3 manieren om absoluut zeker te zijn.
Gegeven: Set A = (1, 2, 3, 4) en set B = (5, 6, 7, 8), en set C = (9)
Bij meting #1 vinden we dat set A zwaarder is dan set B.
Volgens jouw oplossing gooien we de Sets B en C weg en splitsen we Set A door 1 van de knikkers te isoleren -- dus nu: Set A=(1, 2), Set B=(3), en Set C=(4).
Aangezien je een set van 2 knikkers niet kunt vergelijken met een set van 1 knikker... blijven we over met het vergelijken van B & C in Meting #2. Als een van beide zwaarder is, geweldig ... het probleem is opgelost. Echter, als ze in evenwicht zijn, dan weten we dat de zware knikker in set A.... zit en dat betekent dat we meting #3 moeten doen.
#0 #1 #2
#3 #4 #5
#6 #7 #8
Eerst vergelijken we het gewicht van de linkermunten (#0 #3 #6) vs de rechtermunten (#2 #5 #8) zodat we weten of de zwaarste munt links, in het midden of rechts ligt. Dan vergelijken we het gewicht van de bovenste munten (#0 #1 #2) vs de onderste munten (#6 #7 #8) zodat we weten of de zwaarste munt boven, in het midden of onder ligt. Dan vinden we de munt door middel van coördinaten.