つまり、9個のビー玉と天秤がある。あるいは体重計。あるいは重量バランス。呼び方は何でもいい。
本質的にはこれだ。
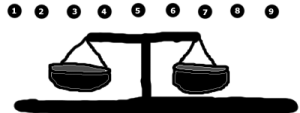
2歳児のような絵なので、上の絵について少し説明します。本物の天秤(またははかり)は、私が上に描いた器具に少し似ています。小さな「バケツ」に物を入れると、天秤は重い方に傾きます。
ええ、おそらく絵を描く必要もなかったかもしれません。いずれにしても、謎を解きましょう。
1) あなたは9個のビー玉を持っています(見たままの状態)。
2) そのうち8個は、まったく同じ重さです。残りの1個は、他のものよりわずかに重いです。あなたは、どれがどれだかわかりません。
3) 計量器を使用/設定できるのは合計2回までです。つまり、ここで2回の測定(または「比較」)を行うことができます。
4) 各「バケツ」には複数のビー玉を入れる十分なスペースがあります。それぞれの側に同じ数のビー玉がある限り、重いビー玉は、その側にある計量器を傾けるのに十分な重さだけです。
重いビー玉はどのように見つけますか?
ヒントと答えは下までスクロールして!.
.
.
.
ヒント #1: 最初の測定では、ビー玉をすべて入れるわけではありません(奇数個のビー玉しかないので、それはできません!)。少なくとも1個は残しておきます。.
.
.
.
ヒント #2: 明らかに、最初の測定では、各面に偶数のビー玉を置かなければなりません。つまり、1+1、2+2、3+3、または4+4のいずれかです。1個の重いビー玉を除いて、すべてのビー玉は同じ重さであることを忘れないでください。これは重要な情報です。.
.
.
.
ヒント #3:一度に比較できるビー玉のグループはいくつあるでしょうか?もし2つと答えたなら、もう一度考えてみてください!.
.
.
.
ヒント #4 (大きなヒントで、答えの一部):ビー玉が3個しかないと仮定し、天秤は1回しか使えないとします。3個のうちどれが重いのか見分けられますか?(答えはイエスです)。どうやって?.
.
.
.
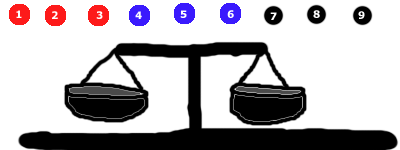
ヒント #5:以下にいくつかの色を用意しました。.
..
.
ビー玉を3つのグループに分けてみました。 行き詰まった場合は、最初の測定にこの写真が役立つかもしれません。.
.
….
ヒント #6: 次の画像(第1の測定の解答)は以下です。.
.
.
.
まず、それぞれの面にビー玉を3つずつ入れます。この場合、黒い玉は除きます。
3つのうちの1つが起こります。
- 赤い面が下がる(この場合、赤いグループに最も重いビー玉が入っていることが分かります)。または
- 青い面が下がる可能性もあります(その場合は、青いグループに最も重いビー玉が入っていることが分かります)。または
- 両側がバランスする(この場合、黒いグループに重いビー玉が含まれていることが分かります)
いずれにしても、最初の測定で9つの可能性から3つに絞り込むことができました。
続けていきましょう。.
.
..
議論のために、上記の測定で重いビー玉が入っていたのが青いビー玉だったと仮定しましょう。2回目で最後の測定を行ってみましょう。
最初にやったときと同様に、これらを均等に3つのグループに分けます(今回は3つのグループに1つずつ)。
3つのうちの1つが再び起こります。
- もし#4が落ちれば、それは重いものであることが分かります
- もし#5が落ちれば、それは重いものであることが分かります
- 天秤が釣り合えば、#6 が重いとわかる!
さらに考えてみよう(簡単すぎた場合は!):
重い大理石を見つけるには2回の測定が必要でした。27個のビー玉(26個は同じ重さで、1個はそれより重い)があった場合、何回の測定が必要でしょうか?
81個のビー玉(80個は同じ重さで、1個はそれより重い)があった場合はどうでしょうか?
さて、これは2006年以来初めて投稿した頭の体操問題です(7年も経ったのか…)。楽しんでいただけたでしょうか!


ビー玉を1つ取り除き、4つと4つを片側に置きます。バランスが取れている場合は、取り外したものが最も重いです。
バランスが崩れている場合は、重い方から4つを選択します。1つを取り外して分離します。
その 1 つを、除外されたため最初に削除したものと置き換えます。そして、2と2で2番目の測定を行います。バランスが取れている場合は、分離したものが最も重いです。
彼らが既知の大理石を置き換えた側でバランスが崩れている場合。最も重いものを識別できます。
彼らが2つの未知の上で不均衡な場合、正しく選択する確率は50/50になります。このソリューションは、絶対に確信できる3つの方法を提供します。
セットA =(1、2、3、4)、セットB =(5、6、7、8)、およびセットC =(9)
測定#1では、セットAがセットBよりも重いことがわかります
あなたの解決策に従って、セットBとCを破棄し、ビー玉の1つを分離してセットAを分割します-つまり、セットA =(1、2)、セットB =(3)、およびセットC =(4)。
ビー玉2個とビー玉1個を比較できないので...あとは、測定#2のBとCを比較するだけです。 どちらかが重いなら、素晴らしいです...問題は解決しました。 しかし、バランスが取れていれば、重いビー玉がセットAにあることがわかります。そしてそれは、測定#3を作ることを意味します。
コインは次のように配置されています。
#0 #1 #2
#3 #4 #5
#6 #7 #8
まず、左のコイン(#0 #3 #6)と右のコイン(#2 #5 #8)の重量を比較します
したがって、最も重いコインが左、中央、または右のいずれにあるかがわかります。
次に、上のコイン(#0 #1 #2)と下のコイン(#6 #7 #8)の重量を比較します
したがって、最も重いコインが上部、中央、または下部のいずれにあるかがわかります。
次に、座標でコインを見つけます。