昔々、強力な王が治める強力な王国がありました。この王は、自らがその国で最も偉大で賢明な人物であると思われたかったのです。しかし残念なことに、王の民は王を尊敬していませんでした。むしろ、困った時には、その国の土地に住む4人の賢者たちに頼るのでした。一般的に、賢者たちは王よりも賢いとみなされており、王はこれを非常に気に病んでいました。

通常であれば、王は彼らを処刑するよう命じるだけでよかった。しかし、王はそれが民衆を大いに動揺させることを知っていた。そこで王は、賢者たちを出し抜き、彼らが民衆が信じているほど賢くないことを証明する計画を思いついた。民衆が解決できない問題で彼らを公に辱めた後、王は民衆が彼らの命を奪うという王の決定をより容易に受け入れるだろうと考えた。

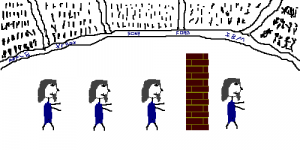
王は、中庭に観覧席を設け、中央に頑丈なレンガの壁を築くよう命じた。そして賢者たちを呼び寄せ、彼らを次の位置に配置させた。彼らはそれぞれ自分の位置と他の3人の位置を知っていた。

王は次のように言った。

諸君がここにいるのは、諸君が自分こそが最も賢いと主張しているからだ。しかし、これから行うテストで、その主張が誤りであることを証明しよう。まもなく、諸君は目隠しをされる。目隠しをされた状態で、それぞれの頭上に帽子が置かれる。赤い帽子と緑の帽子がそれぞれ2つずつある。帽子が頭に置かれたら、目隠しが外される。自分の頭に乗せられた帽子の色を見ることはできませんし、後ろの人のかぶっている帽子の色を見ることもできません。 常に前を向いていなければならず、動いたり、振り返ったりしてはいけません。 さらに難しくするために、あなた方のうちの1人はレンガの壁を隔てて離れ、互いに相手の姿を見ることができず、相手もこちらを見ることができないようにします。 私の質問に答える以外は、一切、話したり、コミュニケーションをとったりしてはいけません。

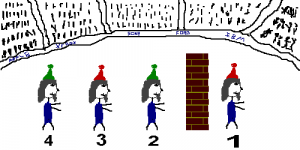
王は召使たちに、このように男たちに帽子をかぶらせた。

王はさらに話を続けた。

「あなた方の中の誰かが答えなければならない質問は、『あなたの帽子の色は何色ですか?』です。答えられるのはただ一人だけです。正しく答えられた場合は、あなた方は全員助かります。間違って答えられた場合は、あなた方は全員死にます。私の質問に答える以外は、話したり、動いたり、あるいは何らかの方法で意思疎通を図ったりしてはいけません。また、緑色の帽子と赤色の帽子はそれぞれ2つずつあることを覚えておいてください。必要なだけ時間をかけてください。

しばらくして、賢者の一人が答えました。彼は自分の答えに自信を持っており、正解でした。信じられないほどの知性に困惑した王は、彼ら全員を解放せざるを得ませんでした。

さて、皆さんの質問は以下の通りです。

1. 誰が答えたのか?
2. 彼らはどうやって自分の帽子の色を知ったのか?

–

答えは下記です

–

ヒントその1: 彼らがそれぞれ何を見ているか考えてみてください。

ヒント1の答え:賢者1号は何も見えない。2号も同様だ。賢者3号は目の前の人を見ることができ、賢者4号は目の前の2人を見ることができる。

–

ヒントその2:もし彼らがそれぞれ確率に基づいて推測するとしたら、それぞれ何を推測するでしょうか?

ヒント2の答え:賢者1と2は何も見えないので、緑か赤のどちらかになる確率は50%です。賢者 #3 は目の前に緑の帽子があるのを見ます。 したがって、緑の帽子が1つ、赤い帽子が2つ残っていることが分かります。 この確率に基づいて、彼が赤い帽子である可能性は66%です。 賢者 #4 は目の前に緑の帽子と赤い帽子の両方を見ます。 緑の帽子が1つ、赤い帽子が1つ残っているので、どちらになる可能性も50%です。

–

ヒントその3(答えの一部):賢者 #3 が答えます。この場合、「赤」と答えます。もちろん、彼は正解です。いいえ、彼は当てずっぽうで答えたわけではありません。では、どうして彼は知っていたのでしょうか?

–

ヒントその4: 彼がすぐに答えなかったことを思い出してください。「しばらくして、彼らのうちの一人が答えました」と書いてあります。なぜ彼はすぐに答えなかったのでしょうか?

–

ヒントその5: 3番目と4番目の賢者だけが何かを見ることができました。彼らが見ることができるものに基づいて、どのような組み合わせが考えられますか?

答え:

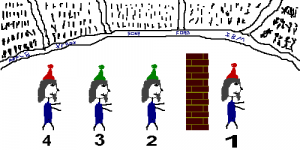
賢者3と4に共通しているのは、2人とも賢者2が緑色であると見ていることです。しばらく待つと、賢者3は自分が緑色ではないことが分かります。もし彼が緑色であったなら、これは唯一の可能な組み合わせ(赤い帽子が2つ、緑の帽子が2つ)となります。

もしそうであれば、賢者4番は緑の帽子を2つ見たことになり、緑の帽子は2つしかないので、賢者4番は「赤」と答えるでしょう。基本的に、2番と3番が同じ色であれば、4番は反対の色を答えることになります。

4番が答えなかったので、3番は自分が2番と反対の色であるとわかり、自信を持って正解を答えることができました!