Quindi, avete 9 biglie e una bilancia. O bilancia dei pesi. O bilancia dei pesi. O come volete chiamarla.
In sostanza, questo:
Il mio fantastico disegno di una bilancia a peso e 9 biglie
Dato che disegno come un bambino di 2 anni, vorrei fare alcune precisazioni su ciò che vedete qui sopra. Una vera bilancia pesapersone (o bilancia) assomiglia un po’ all’apparecchio che ho disegnato qui sopra. Si possono mettere degli oggetti nei piccoli “secchi” e la bilancia si inclinerà verso il lato più pesante.
Sì, probabilmente non avrei dovuto nemmeno preoccuparmi di fare il disegno. In ogni caso, passiamo all’indovinello.
1) Avete 9 biglie (come si vede).
2) 8 di esse hanno esattamente lo stesso peso. La biglia rimanente è poco più pesante delle altre. Non sapete quale sia.
3) Potete usare/regolare la bilancia DUE volte in totale. In altre parole, si possono effettuare 2 misurazioni (o “confronti”).
4) Ogni “secchio” ha spazio sufficiente per più biglie. Finché si ha lo stesso numero di biglie in ogni lato, la biglia pesante ha un peso sufficiente a far pendere la bilancia da un lato.
Come si fa a trovare la biglia pesante?
(scorrete lentamente verso il basso per i suggerimenti e per trovare eventualmente la risposta!)
.
.
.
.
Consiglio #1: Non metterete tutte le biglie per la prima misurazione (non funzionerebbe perché abbiamo un numero dispari!). Ne lascerete almeno 1 da parte.
.
.
.
.
Consiglio n. 2: È chiaro che per la prima misura si deve mettere un numero pari di biglie in ogni lato. Quindi o 1+1, o 2+2, o 3+3, o 4+4. Non dimenticate che tutte le biglie hanno lo stesso peso, tranne quella più pesante (1). Questa è una chicca importante.
.
.
.
.
Consiglio #3: Quanti gruppi di biglie si possono confrontare contemporaneamente? Se avete detto 2, ripensateci!
.
.
.
.
Consiglio #4 (importante e parte della risposta): Fate finta di avere solo 3 biglie, ma di poter usare la bilancia solo una volta. Riuscireste a capire quale delle 3 è quella più pesante? (la risposta è sì). Come?
.
.
.
.
Consiglio #5: qui sotto ci sono alcuni colori per aiutarvi….
.
.
.
.
Abbiamo diviso le biglie in 3 gruppi. Se vi siete bloccati, l’immagine potrebbe aiutarvi con la prima misurazione.
.
.
.
.
Consiglio #6: L’immagine successiva (soluzione alla prima misura) è qui sotto:
.
.
.
.
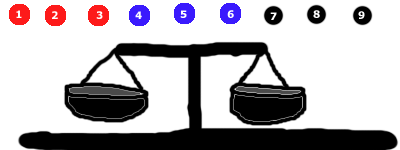
Iniziare mettendo 3 biglie in ogni lato. In questo caso, lasciamo fuori quelle nere.
Succederà una delle 3 cose:
- il rosso può scendere (in questo caso sappiamo che il gruppo gruppo rosso contiene la biglia più pesante), oppure
- Il blu può scendere (in tal caso sappiamo che il gruppo gruppo blu contiene la biglia più pesante), oppure
- I lati si equilibreranno (nel qual caso sappiamo che il gruppo nero deve contenere la biglia più pesante)
.
In ogni caso, abbiamo ristretto il campo da 9 possibilità a 3 con la prima misurazione.
Continuiamo.
.
.
.
.
Per amor di discussione, facciamo finta che siano state le biglie blu ad avere il peso maggiore nella misurazione precedente. Prendiamo la nostra seconda e ultima misurazione.
Come la prima volta, le dividiamo equamente in 3 gruppi (3 gruppi di UNO questa volta).
Anche in questo caso si verificherà una delle tre cose:
- Se #4 scende, sappiamo che è quello pesante
- Se #5 scende, sappiamo che è quello pesante
- Se la bilancia si bilancia, sappiamo che #6 deve essere quello pesante!
Un’ulteriore riflessione (se è stata troppo facile per voi!):
Per trovare la biglia pesante sono state necessarie 2 misure. Di quante misure avremmo bisogno se avessimo 27 biglie (26 dello stesso peso e 1 più pesante)?
E se avessimo 81 biglie (80 di peso uguale e 1 più pesante)?
–
Questo è il primo rompicapo che pubblico dal 2006 (7 anni…). Spero che vi sia piaciuto!


Togliete una biglia e mettetene quattro e quattro per lato. Se sono in equilibrio, quella rimossa è la più pesante.
Se sono sbilanciate, selezionate le quattro dal lato più pesante. Rimuovetene una e isolatela.
Sostituitelo con quello rimosso in origine perché è stato escluso. Eseguite la seconda misura con due e due. Se sono equilibrati, quello che avete isolato è il più pesante.
Se sono sbilanciate, dal lato in cui avete sostituito la biglia nota. È possibile identificare la più pesante.
Se sono sbilanciate sui due lati sconosciuti, avrete il 50% di possibilità di scegliere correttamente. Questa soluzione fornisce 3 modi per essere assolutamente sicuri.
Dato: Set A = (1, 2, 3, 4) e Set B = (5, 6, 7, 8), e Set C = (9)
Sulla misura numero 1, troviamo che l'insieme A è più pesante dell'insieme B.
Come da soluzione, scartiamo gli insiemi B e C e dividiamo l'insieme A isolando 1 delle biglie - quindi ora: Insieme A=(1, 2), Insieme B=(3) e Insieme C=(4).
Poiché non è possibile confrontare un insieme di 2 biglie con un insieme di 1 biglia... non resta che confrontare B e C nella misura n. 2. Se una delle due è più pesante, il problema è risolto. Tuttavia, se sono in equilibrio, sappiamo che la biglia pesante si trova nell'insieme A.... e questo significa fare la misura #3.
#0 #1 #2
#3 #4 #5
#6 #7 #8
Per prima cosa, confrontiamo il peso delle monete di sinistra (#0 #3 #6) rispetto a quelle di destra (#2 #5 #8) in modo da sapere se la moneta più pesante si trova a sinistra, al centro o a destra. Poi, confrontiamo il peso delle monete in alto (#0 #1 #2) rispetto a quelle in basso (#6 #7 #8) in modo da sapere se la moneta più pesante si trova in alto, al centro o in basso. Poi troviamo la moneta in base alle coordinate.