तो, आपके पास 9 कंचे और एक तराजू है। या वज़न मापने का पैमाना। या वज़न मापने का तराजू। या जो भी आप इसे कहना चाहें।
मूलतः, यह:
वजन संतुलन और 9 पत्थरों का मेरा अद्भुत चित्र
चूँकि मैं 2 साल के बच्चे की तरह चित्र बनाता हूँ, इसलिए ऊपर जो आप देख रहे हैं, उसके बारे में कुछ स्पष्टीकरण। एक वास्तविक वज़न संतुलन (या पैमाना) थोड़ा-बहुत उस उपकरण जैसा दिखता है जिसे मैंने ऊपर बनाया है। आप छोटी-छोटी “बाल्टी” में चीज़ें रख सकते हैं और तराजू भारी तरफ़ झुक जाएगा।
हाँ, शायद मुझे तस्वीर के बारे में सोचना भी नहीं चाहिए था। खैर, अब पहेली पर आते हैं ।
1) आपके पास 9 कंचे हैं (जैसा कि दिखाया गया है)।
2) उनमें से 8 का वज़न बिल्कुल एक जैसा है। बचा हुआ मार्बल बाकी से थोड़ा भारी है । आपको नहीं पता कि कौन सा मार्बल कौन सा है।
3) आपको कुल मिलाकर दो बार स्केल का उपयोग/सेट करने की अनुमति है। दूसरे शब्दों में, आपको यहाँ 2 माप (या “तुलना”) लेने की अनुमति है।
4) प्रत्येक “बाल्टी” में कई मार्बल्स के लिए पर्याप्त जगह होती है। जब तक आपके पास प्रत्येक तरफ समान संख्या में मार्बल्स हैं, तब तक भारी मार्बल में तराजू को अपनी तरफ झुकाने के लिए पर्याप्त वजन होता है।
आप भारी संगमरमर कैसे ढूंढते हैं?
(सुझावों और अंततः उत्तर तक पहुंचने के लिए धीरे-धीरे नीचे स्क्रॉल करें!)
.
.
.
.
संकेत देना #1: आपआप अपने पहले माप के लिए सभी मार्बल नहीं डालेंगे (यह काम नहीं करेगा क्योंकि हमारे पास विषम संख्या है!)। आप कम से कम 1 को अलग रखेंगे।
.
.
.
.
संकेत देना #2: स्पष्ट रूप से, आपको अपने पहले माप के लिए प्रत्येक पक्ष में सम संख्या में मार्बल्स डालने होंगे। तो या तो 1+1, 2+2, 3+3, या 4+4। मत भूलिए, 1 भारी मार्बल को छोड़कर सभी मार्बल्स का वजन समान है। यह एक महत्वपूर्ण जानकारी है।
.
.
.
.
संकेत देना #3 : आप एक बार में कितने मार्बल्स के समूहों की तुलना कर सकते हैं? अगर आपने 2 कहा है, तो दोबारा सोचें!
.
.
.
.
संकेत देना #4 (एक बड़ा और उत्तर का हिस्सा) : मान लीजिए कि आपके पास केवल 3 मार्बल हैं, लेकिन आप स्केल का उपयोग केवल एक बार कर सकते हैं। क्या आप पता लगा सकते हैं कि 3 में से कौन सा भारी है? (उत्तर हाँ है)। कैसे?
.
.
.
.
संकेत देना #5: नीचे कुछ रंग दिए गए हैं जो आपकी मदद करेंगे…
.
.
.
.
हमने मार्बल्स को 3 समूहों में विभाजित किया है। यदि आप अटक गए हैं, तो चित्र आपकी पहली माप में आपकी मदद कर सकता है।
.
.
.
.
संकेत देना #6: अगली छवि (पहली माप का समाधान) नीचे है:
.
.
.
.
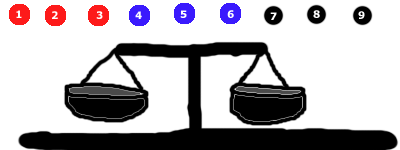
प्रत्येक पक्ष में 3 मार्बल रखकर शुरू करें। इस मामले में, हम काले वाले को छोड़ देते हैं।
तीन में से एक बात घटित होगी:
- लाल पक्ष नीचे जा सकता है (जिस स्थिति में हम जानते हैं कि लाल समूह में सबसे भारी मार्बल है), या
- नीला पक्ष नीचे जा सकता है (जिस स्थिति में हम जानते हैं कि नीले समूह में सबसे भारी मार्बल है), या
- दोनों पक्ष संतुलित हो जाएंगे (जिस स्थिति में हम जानते हैं कि काले समूह में भारी मार्बल होना चाहिए)
किसी भी तरह से हमने अपने पहले माप में इसे 9 संभावनाओं से घटाकर 3 कर दिया है।
चलिए, चलते रहें।
.
.
.
.
तर्क के लिए, मान लेते हैं कि ऊपर दिए गए माप में नीला मार्बल ही भारी था। चलिए अपना दूसरा और अंतिम माप लेते हैं।
पहली बार की तरह, हमने इन्हें तीन समूहों में बराबर विभाजित किया (इस बार एक के तीन समूह)।
तीन चीजों में से एक फिर घटित होगी:
- यदि #4 नीचे चला जाता है, तो हम जानते हैं कि यह भारी है
- यदि #5 नीचे चला जाता है, तो हम जानते हैं कि यह भारी है
- यदि तराजू संतुलित हो तो हम जानते हैं कि संख्या 6 भारी होगी!
आगे विचार (यदि यह आपके लिए बहुत आसान था!):
भारी मार्बल को खोजने के लिए 2 माप की आवश्यकता थी। यदि हमारे पास 27 मार्बल हों (26 समान वजन के और 1 भारी) तो हमें कितने माप की आवश्यकता होगी?
यदि हमारे पास 81 कंचे हों (80 का वजन सम हो तथा 1 अधिक भारी हो) तो क्या होगा?
–
खैर, यह 2006 (7 साल… ओह!) के बाद से मेरा पहला ब्रेन टीज़र है। लेकिन जल्द ही और भी आने चाहिए। अगर आपको यह दिलचस्प लगा, तो आप नीचे दी गई श्रेणी पर क्लिक करके या साइट के शीर्ष पर मेनू में इसे ढूँढ़कर “पहेलियाँ, पहेलियाँ, ब्रेन टीज़र” अनुभाग पर जा सकते हैं।


* हम पहले 3 के समूह में पत्थर डालते हैं। हम देखना चाहते हैं कि किस समूह में भारी संगमरमर है। ऐसा करने के लिए, प्रत्येक पक्ष में 3 पत्थर डालें (3 बाएं, 3 दाएं, 3 अप्रयुक्त)
* यदि स्केल एक तरफ की ओर इशारा करता है, तो हम जानते हैं कि 3 के समूह में भारी संगमरमर है। यदि यह एक तरफ टिप नहीं करता है (यदि यह संतुलित है), तो हम जानते हैं कि 3 के "अप्रयुक्त" समूह में भारी संगमरमर है। 3 मार्बल्स का भारी समूह रखें और बाकी को त्याग दें।
* चूंकि अब हमारे पास 3 मार्बल्स हैं (जिनमें से 1 भारी है), प्रत्येक पक्ष में 1 रखें (1 बाएं, 1 दाएं, 1 अप्रयुक्त)
* पैमाने फिर से सेट करें। यदि यह एक तरफ जाता है, तो हम जानते हैं कि संगमरमर भारी है! यदि इसके बजाय यह संतुलित होता है, तो हम जानते हैं कि एक "अप्रयुक्त" संगमरमर भारी है!
एक संगमरमर निकालें और प्रत्येक तरफ चार और चार एक डालें। यदि वे संतुलित हैं, तो आपके द्वारा हटाया गया सबसे भारी है।
यदि वे असंतुलित हैं, तो भारी पक्ष से चार का चयन करें। एक को हटा दें और अलग कर दें।
उस एक को उस व्यक्ति से बदलें जिसे आपने मूल रूप से हटा दिया था क्योंकि इसे खारिज कर दिया गया है। और अपना दूसरा उपाय दो और दो के साथ करें। यदि वे संतुलित हैं, तो आपने जो अलग किया है वह सबसे भारी है।
यदि वे उस तरफ असंतुलित हैं जहां आपने ज्ञात संगमरमर को प्रतिस्थापित किया था। आप सबसे भारी की पहचान कर सकते हैं।
यदि वे 2 अज्ञात पर असंतुलित हैं, तो आपके पास सही ढंग से चुनने का 50/50 मौका होगा। यह समाधान 3 तरीके प्रदान करता है जिनसे आप पूरी तरह से सुनिश्चित हो सकते हैं।
दिया गया है: समूह A = (1, 2, 3, 4) और समूह B = (5, 6, 7, 8), और समूह C = (9)
मापन # 1 पर, हम पाते हैं कि सेट ए सेट बी से भारी है
आपके समाधान के अनुसार, हम सेट बी और सी को त्याग देते हैं और 1 मार्बल्स को अलग करके सेट ए को विभाजित करते हैं - इसलिए अब: सेट ए = (1, 2), सेट बी = (3), और सेट सी = (4)।
चूंकि आप 1 मार्बल के सेट के खिलाफ 2 मार्बल्स के सेट की तुलना नहीं कर सकते ... हम माप # 2 में बी और सी की तुलना करने के साथ छोड़ दिए गए हैं। यदि उनमें से कोई भी भारी है, तो महान... समस्या हल हो गई है। हालांकि, अगर वे संतुलित हैं, तो हम जानते हैं कि भारी संगमरमर सेट ए में है .... और इसका मतलब है कि मापन # 3 बनाना।
सिक्कों को इस तरह व्यवस्थित किया जाता है:
#0 #1 #2
#3 #4 #5
#6 #7 #8
सबसे पहले, हम बाएं सिक्कों के वजन (#0 #3 #6) बनाम दाएं सिक्कों (#2 #5 #8) की तुलना करते हैं
तो हम जानते हैं कि सबसे भारी सिक्का बाएं, मध्य या दाएं में है या नहीं।
फिर, हम शीर्ष सिक्कों के वजन (#0 #1 #2) बनाम नीचे के सिक्कों (#6 #7 #8) की तुलना करते हैं
तो हम जानते हैं कि सबसे भारी सिक्का ऊपर, मध्य या नीचे है या नहीं।
फिर हम निर्देशांक द्वारा सिक्का पाते हैं।