Donc, vous avez 9 billes et une balance. Ou une balance de poids. Ou une balance. Ou peu importe comment vous voulez l’appeler.
Essentiellement, ceci :
Mon impressionnant dessin d’une balance de poids et de 9 billes
Parce que je dessine comme un enfant de 2 ans, quelques précisions sur ce que vous voyez ci-dessus. Une vraie balance ressemble un peu à l’appareil que j’ai dessiné ci-dessus. Vous pouvez mettre des choses dans les petits « seaux » et la balance basculera vers le côté le plus lourd.
Oui, je n’aurais probablement pas dû m’embêter avec cette image. En tout cas, passons à l’énigme.
1) Vous avez 9 billes (comme sur la photo).
2) 8 d’entre elles ont exactement le même poids. Le marbre restant est légèrement plus lourd que les autres. Vous ne savez pas lequel est lequel.
3) Vous êtes autorisé à utiliser/régler la balance DEUX FOIS au total. En d’autres termes, vous devez prendre 2 mesures (ou « comparaisons ») ici.
4) Chaque « seau » a suffisamment de place pour plusieurs billes. Tant que vous avez le même nombre de billes de chaque côté, la lourde bille a juste assez de poids pour faire basculer la balance sur le côté.
Comment trouver le marbre lourd ?
(Faites défiler lentement vers le bas pour trouver des conseils et éventuellement la réponse !)
.
.
.
.
CONSEIL n°1 : Vous ne mettrez pas toutes les billes pour votre première mesure (cela ne marcherait pas car nous avons un nombre impair !). ). Vous en laisserez au moins une de côté.
.
.
.
.
CONSEIL n°2 : Il est évident que vous devez mettre un nombre pair de billes de chaque côté pour votre première mesure. Soit 1+1, 2+2, 3+3 ou 4+4. N’oubliez pas que toutes les billes ont le même poids, sauf la plus lourde. C’est une information importante.
.
.
.
.
CONSEIL n° 3 : Combien de groupes de billes pouvez-vous comparer à la fois ? Si vous avez dit 2, réfléchissez bien !
.
.
.
.
CONSEIL n° 4 (un gros, et une partie de la réponse) : Imaginez que vous n’avez que 3 billes, mais que vous ne pouvez utiliser la balance qu’une seule fois. Pouvez-vous déterminer laquelle des 3 était la plus lourde ? (la réponse est oui). Comment ?
.
.
.
.
CONSEIL n° 5 : voici quelques couleurs pour vous aider….
.
.
.
.
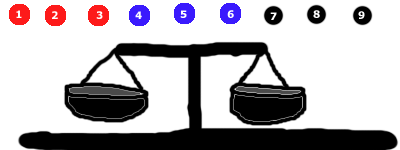
Nous avons séparé les billes en 3 groupes. Si vous étiez bloqué, la photo pourrait vous aider pour votre première mesure.
.
.
.
.
Conseil n°6 : l’image suivante (solution à la 1ère mesure) se trouve ci-dessous :
.
.
.
.
Commencez par mettre 3 billes dans chaque côté. Dans ce cas, on laisse les noires de côté.
Une des trois choses suivantes se produira :
- Le côté rouge peut descendre (dans ce cas, nous savons que le groupe rouge contient la bille la plus lourde), ou
- Le côté bleu peut descendre (auquel cas nous savons que le groupe bleu contient le marbre le plus lourd), ou
- Les côtés s’équilibreront (auquel cas nous savons que le groupe noir doit contenir le marbre lourd)
Quoi qu’il en soit, nous avons réduit le nombre de possibilités de 9 à 3 lors de notre première mesure.
Continuons.
.
.
.
.
Pour les besoins de l’argumentation, imaginons que ce sont les billes bleues qui ont le plus de poids dans la mesure ci-dessus. Prenons notre deuxième et dernière mesure.
Comme la première fois, nous les avons divisés en trois groupes (trois groupes de UN cette fois).
L’une des trois choses suivantes se produira à nouveau :
- Si le n°4 tombe, nous savons que c’est le plus lourd
- Si le n°5 tombe, nous savons que c’est le plus lourd
- Si la balance balance, nous savons que le n°6 doit être le plus lourd !
Réflexion approfondie (si c’était trop facile pour vous !):
Pour trouver le marbre lourd, il a fallu prendre 2 mesures. De combien de mesures aurions-nous besoin si nous avions 27 billes (26 étant du même poids et 1 étant plus lourde) ?
Et si nous avions 81 billes (80 étant du même poids et 1 étant plus lourde) ?
–
Eh bien, c’est le premier casse-tête que j’ai mis en ligne depuis 2006 (7 ans… ah oui !). Mais d’autres devraient venir bientôt. Si vous avez trouvé celui-ci intéressant, vous pouvez accéder à la section « Enigmes, puzzles, casse-tête » en cliquant sur la catégorie ci-dessous ou en la trouvant dans le menu en haut du site.


Retirez une bille et mettez-en quatre et quatre de chaque côté. Si elles sont équilibrées, celle que vous avez retirée est la plus lourde.
Si elles ne sont pas équilibrées, choisissez la quatre du côté le plus lourd. Retirez une bille et isolez-la.
Remplacez celle-ci par celle que vous avez retirée à l'origine car elle a été exclue. Et faites votre deuxième mesure avec deux et deux. S'ils sont équilibrés, celui que vous avez isolé est le plus lourd.
S'ils sont déséquilibrés du côté où vous avez remplacé le marbre connu. Vous pouvez identifier le plus lourd.
S'ils sont déséquilibrés sur les 2 inconnus, vous aurez une chance sur deux de choisir correctement. Cette solution vous offre 3 moyens d'être absolument sûr.
Étant donné : Ensemble A = (1, 2, 3, 4), ensemble B = (5, 6, 7, 8) et ensemble C = (9).
Lors de la première mesure, nous constatons que l'ensemble A est plus lourd que l'ensemble B.
Selon votre solution, nous éliminons les ensembles B et C et nous divisons l'ensemble A en isolant une des billes - donc maintenant : Ensemble A=(1, 2), Ensemble B=(3), et Ensemble C=(4).
Puisque vous ne pouvez pas comparer un ensemble de 2 billes à un ensemble d'une bille... il ne nous reste plus qu'à comparer B & C dans la mesure n°2. Si l'une d'entre elles est plus lourde, c'est parfait... le problème est résolu. Cependant, si elles sont équilibrées, nous savons alors que la bille la plus lourde se trouve dans le jeu A.... et cela signifie qu'il faut faire la mesure n°3.
Les pièces sont disposées comme suit :
#0 #1 #2
#3 #4 #5
#6 #7 #8
Tout d'abord, nous comparons le poids des pièces de gauche (#0 #3 #6) à celui des pièces de droite (#2 #5 #8).
afin de savoir si la pièce la plus lourde se trouve à gauche, au milieu ou à droite.
Ensuite, nous comparons le poids des pièces du haut (#0 #1 #2) à celui des pièces du bas (#6 #7 #8)
afin de savoir si la pièce la plus lourde se trouve en haut, au milieu ou en bas.
Ensuite, nous trouvons la pièce par coordonnées.