Entonces, tienes 9 canicas y una balanza. O una balanza. O una balanza de peso. O como quieras llamarlo.
Esencialmente, esto:
Mi impresionante dibujo de una balanza de peso y 9 canicas
Porque dibujo como un niño de 2 años, alguna aclaración sobre lo que ves arriba. Una balanza real se parece un poco al aparato que dibujé arriba. Puedes poner cosas en los pequeños «cubos» y la balanza se inclinará hacia el lado más pesado.
Sí, probablemente no debería haberme molestado con el dibujo. En cualquier caso, sobre el enigma.
1) Tienes 9 canicas (como se ve).
2) 8 de ellas tienen exactamente el mismo peso. La canica restante es ligeramente más pesada que las otras. No sabes cuál es cuál.
3) Se te permite usar/ajustar la balanza DOS veces en total. En otras palabras, puedes tomar 2 medidas (o «comparaciones») aquí.
4) Cada «cubo» tiene suficiente espacio para múltiples canicas. Mientras tengas el mismo número de canicas en cada lado, la canica pesada tiene el peso justo para inclinar la balanza hacia su lado.
¿Cómo encuentras la canica pesada?
(¡Descubre lentamente las pistas y finalmente la respuesta!)
.
.
.
.
CONSEJO #1: No pondrás todas las canicas para tu primera medición (¡eso no funcionaría porque tenemos un número impar!). Dejarás por lo menos 1 a un lado.
.
.
.
.
CONSEJO #2: Claramente, tienes que poner un número par de canicas en cada lado para tu primera medición. Así que o bien 1+1, 2+2, 3+3, o 4+4. No olvides que todas las canicas tienen el mismo peso excepto la 1 más pesada. Es un dato importante.
.
.
.
.
CONSEJO #3: ¿Cuántos grupos de canicas puedes comparar a la vez? Si dijiste 2, ¡piénsalo de nuevo!
.
.
.
.
CONSEJO #4 (uno grande, y parte de la respuesta): Imagina que sólo tienes 3 canicas, pero sólo puedes usar la escala una vez. ¿Podrías averiguar cuál de las 3 era la más pesada? (la respuesta es sí). ¿Cómo?
.
.
.
.
CONSEJO #5: abajo hay algunos colores para ayudarte….
.
.
.
.
Hemos separado las canicas en 3 grupos. Si estuvieras atascado, la imagen podría ayudarte con tu primera medición.
.
.
.
.
Consejo #6: La siguiente imagen (solución a la primera medición) está abajo:
.
.
.
.
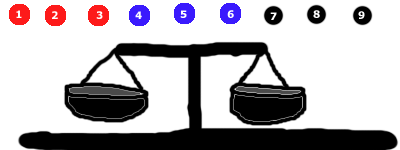
Empieza poniendo 3 canicas en cada lado. En este caso, dejamos las negras fuera.
Una de las 3 cosas que sucederá:
- El lado rojo puede bajar (en cuyo caso sabemos que el grupo rojo contiene la canica más pesada), o
- El lado azul puede bajar (en cuyo caso sabemos que el grupo azul contiene el mármol más pesado), o
- Los lados se equilibrarán (en cuyo caso sabemos que el grupo negro debe contener el mármol pesado)
De cualquier manera lo hemos reducido de 9 posibilidades a 3 en nuestra primera medición.
Sigamos adelante.
.
.
.
.
Por el bien del argumento, pretendamos que eran las canicas azules las que tenían el pesado en la medida de arriba. Tomemos nuestra segunda y última medida.
Al igual que la primera vez, los dividimos en 3 grupos (3 grupos de UNO esta vez).
Una de tres cosas sucederá de nuevo:
- Si el número 4 cae, sabemos que es el pesado
- Si el número 5 cae, sabemos que es el pesado
- Si la balanza se balancea, sabemos que el número 6 debe ser el más pesado.
Pensándolo bien (¡si eso fuera demasiado fácil para ti!):
Para encontrar el mármol pesado se tomaron 2 medidas. ¿Cuántas medidas necesitaríamos si tuviéramos 27 canicas (26 del mismo peso y 1 más pesada)?
¿Y si tuviéramos 81 canicas (80 de peso parejo y una más pesada)?
–
Bueno, este es el primer rompecabezas que he puesto desde 2006 (7 años… ¡caramba!). Pero pronto vendrán más. Si te parece interesante, puedes acceder a la sección «Acertijos, rompecabezas, rompecabezas» haciendo clic en la categoría de abajo o en el menú de la parte superior del sitio.
Quita una canica y pon cuatro y cuatro una de cada lado. Si están equilibradas, la que has quitado es la más pesada.
Si están desequilibradas, selecciona las cuatro del lado más pesado. Quita una y aísla.
Reemplace esa con la que quitó originalmente porque ha sido descartada. Y haga su segunda medida con dos y dos. Si están equilibrados, el que aisló es el más pesado.
Si están desequilibradas en el lado donde sustituiste el mármol conocido. Puedes identificar la más pesada.
Si están desequilibradas en las dos desconocidas, tendrás un 50/50 de posibilidades de elegir correctamente. Esta solución ofrece 3 formas en las que puedes estar absolutamente seguro.
Dados: Conjunto A = (1, 2, 3, 4) y Conjunto B = (5, 6, 7, 8), y Conjunto C = (9)
En la medida 1, encontramos que el conjunto A es más pesado que el conjunto B
Según su solución, descartamos los conjuntos B y C y dividimos el conjunto A aislando 1 de las canicas -- así que ahora Conjunto A=(1, 2), Conjunto B=(3), y Conjunto C=(4).
Como no se puede comparar un conjunto de 2 canicas contra un conjunto de 1 canica... nos queda sólo comparar B & C en la medida #2. Si cualquiera de ellas es más pesada, genial... el problema está resuelto. Sin embargo, si están equilibradas, entonces sabemos que la canica pesada está en el conjunto A.... y eso significa hacer la Medición #3.