So, jy het 9 albasters en ‘n balans. Of gewigskaal. Of gewigsbalans. Of wat jy dit ook al wil noem.
In wese, dit:
My wonderlike tekening van ‘n gewigsbalans en 9 albasters
Omdat ek teken soos ‘n 2-jarige, ‘n bietjie verduideliking oor wat jy hierbo sien. ‘n Regte gewigsbalans (of skaal) lyk effens soos die apparaat wat ek hierbo geteken het. Jy kan goed in die klein “emmers” sit en die skaal sal na die swaarder kant toe kantel.
Ja, ek moes my seker nie eers aan die prentjie gesteur het nie. In elk geval, op die raaisel .
1) Jy het 9 albasters (soos gesien).
2) 8 van hulle is presies dieselfde gewig. Die oorblywende albaster is effens swaarder as die ander. Jy weet nie wat is watter nie.
3) Jy word toegelaat om die skaal in totaal TWEE KEER te gebruik/stel. Met ander woorde, jy kan hier 2 metings (of “vergelykings”) neem.
4) Elke “emmer” het genoeg plek vir veelvuldige albasters. Solank jy dieselfde aantal albasters aan elke kant het, het die swaar albaster net genoeg gewig om die skaal na sy kant te kantel.
Hoe vind jy die swaar marmer?
(blaai stadig af vir wenke en om uiteindelik die antwoord!)
.
.
.
.
WENK #1: Jysal nie al die albasters insit vir jou eerste meting nie (dit sal nie werk nie, want ons het ‘n onewe getal!). Jy sal ten minste 1 eenkant laat.
.
.
.
.
WENK #2: Dit is duidelik dat jy ‘n ewe aantal albasters aan elke kant moet sit vir jou eerste meting. Dus óf 1+1, 2+2, 3+3 of 4+4. Moenie vergeet nie, al die albasters is dieselfde gewig behalwe die 1 swaarder een. Dit is ‘n belangrike goed.
.
.
.
.
WENK #3 : Hoeveel groepe albasters kan jy gelyktydig vergelyk? As jy 2 gesê het, dink weer!
.
.
.
.
WENK #4 (‘n groot een, en deel van die antwoord) : Maak asof jy net 3 albasters gehad het, maar die skaal net een keer kon gebruik. Kon jy uitvind watter van die 3 die swaar een was? (die antwoord is ja). Hoe?
.
.
.
.
WENK #5: hieronder is ‘n paar kleure om jou te help ….
.
.
.
.
Ons het die albasters in 3 groepe geskei. As jy vas was, kan die prentjie jou dalk help met jou eerste meting.
.
.
.
.
WENK #6: Volgende prent (oplossing vir die 1ste meting) is hieronder:
.
.
.
.
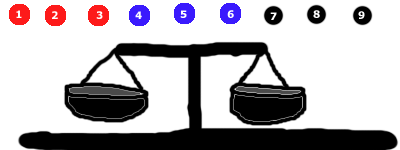
Begin deur 3 albasters aan elke kant te sit. In hierdie geval laat ons die swartes uit.
Een van 3 dinge sal gebeur:
- Die rooi kant kan afgaan (in welke geval ons weet dat die rooi groep die swaarste albaster bevat), of
- Die blou kant kan afgaan (in welke geval ons weet die blou groep bevat die swaarste albaster), of
- Die kante sal balanseer (in welke geval ons weet die swart groep moet die swaar albaster bevat)
Hoe dit ook al sy, ons het dit verminder van 9 moontlikhede tot 3 op ons eerste meting.
Kom ons gaan voort.
.
.
.
.
Ter wille van argument, kom ons maak asof dit die blou albasters was wat die swaar een in die afmeting hierbo gehad het. Kom ons neem ons 2de en laaste meting.
Soortgelyk aan die eerste keer, verdeel ons dit eweredig in 3 groepe (hierdie keer 3 groepe van EEN).
Een van drie dinge sal weer gebeur:
- As #4 afgaan, weet ons dit is die swaar een
- As #5 afgaan, weet ons dit is die swaar een
- As die skaal balanseer, weet ons #6 moet die swaar een wees!
Verdere gedagtes (as dit vir jou te maklik was!):
Om die swaar albaster te vind, het 2 mates geneem. Hoeveel mates sal ons nodig hê as ons 27 albasters het (26 is dieselfde gewig en 1 is swaarder)?
Wat as ons 81 albasters gehad het (80 is ewe in gewig en 1 is swaarder)?
–
Wel, dit is die eerste breinbreker wat ek sedert 2006 opgesit het (7 jaar … jis!). Maar meer behoort binnekort te kom. As jy hierdie een interessant gevind het, kan jy die “Raaisels, raaisels, breinkrakers”-afdeling opslaan deur op die kategorie hieronder te klik of dit in die spyskaart aan die bokant van die webwerf te vind.


* Ons sit eers albasters in groepe van 3. Ons wil sien watter groep die swaar marmer bevat. Om dit te doen, sit 3 albasters in elke kant (3 links, 3 regs, 3 ongebruik)
* As die skaal na 'n kant wys, weet ons dat die groep van 3 die swaar marmer het. As dit nie na 'n kant kantel nie (as dit balanseer), weet ons dat die "ongebruikte" groep van 3 die swaar marmer bevat. Hou die swaar groep van 3 albasters en gooi die res weg.
* Aangesien ons nou 3 albasters het (waarvan 1 die swaar een is), sit 1 aan elke kant (1 links, 1 regs, 1 ongebruik)
* Stel die skaal weer in. As dit na 'n kant toe wys, weet ons dat marmer die swaar een is! As dit eerder balanseer, weet ons die een "ongebruikte" marmer is die swaar een!
Verwyder een marmer en sit vier en vier een aan elke kant. As hulle gebalanseerd is, is die een wat jy verwyder het die swaarste.
As hulle ongebalanseerd is, kies die vier van die swaarder kant. Verwyder een en isoleer.
Vervang daardie een met die een wat jy oorspronklik verwyder het omdat dit uitgesluit is. En doen jou tweede maat met twee en twee. As hulle gebalanseerd is, is die een wat jy geïsoleer het die swaarste.
As hulle ongebalanseerd is aan die kant waar jy die bekende marmer vervang het. Jy kan die swaarste identifiseer.
As hulle ongebalanseerd is op die 2 onbekende, sal jy 'n 50/50 kans hê om korrek te kies. Hierdie oplossing bied 3 maniere waarop jy absoluut seker kan wees.
Gegee: Stel A = (1, 2, 3, 4) en Stel B = (5, 6, 7, 8), en Stel C = (9)
Op meting # 1 vind ons dat stel A swaarder is as stel B
Volgens u oplossing gooi ons stelle B en C weg en verdeel Stel A deur 1 van die albasters te isoleer - dus nou: Stel A = (1, 2), Stel B = (3) en Stel C = (4).
Aangesien u nie 'n stel van 2 albasters met 'n stel van 1 marmer kan vergelyk nie ... ons sit met net die vergelyking van B & C in meting #2. As een van die twee swaarder is, wonderlik ... Die probleem is opgelos. As hulle egter gebalanseerd is, dan weet ons dat die swaar marmer in Stel A is.... en dit beteken om meting #3 te maak.
Die munte is so gerangskik:
#0 #1 #2
#3 #4 #5
#6 #7 #8
Eerstens vergelyk ons die gewig van die linkermuntstukke (#0 #3 #6) teenoor die regte munte (#2 #5 #8)
Ons weet dus of die swaarste muntstuk links, middel of regs is.
Dan vergelyk ons die gewig van die boonste munte (#0 #1 #2) teenoor die onderste munte (#6 #7 #8)
Ons weet dus of die swaarste muntstuk bo, middel of onder is.
Dan vind ons die muntstuk per koördinaat.